Odds and Ends

Chapter 13 but not in text

Email me

Back to:

Unit Organization

• Testing for a difference between variances
  • Confidence Interval
  • known vs. Unknown variances
  • 2 unknown variances
• Calculating Power
• More post-hoc tests for differences between levels in ANOVA analysis
  • Sheffé
• Testing for a difference between proportions
• Other uses for the Chi-square distribution
• A Bit More Probability
• Terminology

Testing for a difference between variances (s²)

There are two situations in which a comparison of two variances might be in order

Situation A - comparing an observed variance to an expected (= known) variance

• this situation may arise when a well known procedure is changed and you want to know if the change has made a difference in the variability of the process
• in manufacturing, it is often important that variation be such that some critical value is rarely exceeded and so the variation of a procedure is critical to consistent success in production

Situation B - comparing two observed variances (neither of which is calculated or known from prior experience)

• this situation might arise when the variance is of greater interest than the mean
• this situation definitely arises when doing a parametric statistical procedure that assumes homoskedasticity (also spelled homoscedasticity) - equality of variances - such as Lecture 11a or 11b

Situation A - Using the s²-square distribution

The Chi-square distribution can be used to construct a confidence interval for a variance or standard deviation or to test the hypothesis that a sample variance does not differ from an expected or known variance.

Confidence interval for a sample variance

Procedure:

• First you have to find the² values for the right and left side of the confidence interval.
  • Since the ² distribution is not symmetrical (especially with small sample sizes) and is never centered over 0, you have to look up either side.
  • This is best seen through an example - say a 95% confidence interval
    • you want to divide the² distribution into three parts -2.5% on the left, 95% in the middle, and 2.5% on the right, which takes two dividing points
    • ² distribution tables typically give the right tail so you want the values for 97.5% (the left side dividing point) and 2.5%
    • the Samuels and Witmer table will only give you values for right tail probabilities up to 20%, so you can't get your left side ² value from that table
    • you can use the Chisquare function in MSExcel or go to the web or come to me to get the left side
  • Degrees of Freedom = n -1      (n is the sample size)
• Now that you have the ² values, you can calculate the confidence interval:

  

• you can get the confidence interval for the standard  deviation by taking the square root of the two confidence interval limits

Hypothesis test of the difference between a sample variance and a known variance

This situation arises when you have a sample and can calculate a sample variance and you want to compare this value with a known variance to see if they are really different or if the difference is just due to sampling error

there are two ways you might know the value of a variance - theory or experience

• there is an expected variance based on a formula derived from statistical theory - expected, here, means that you can calculate what you expect the variance to be
• you have experience with data of the sort found in the sample and you feel that the historical variance is accurate (this is equivalent to accepting the variation published in the literature as the "true and accurate" variance)

There are three alternative hypotheses, each with its own variation of the test

• the first two situations are one-tailed situations for alternative hypotheses that the sample variance is larger than the known variance or that the sample variance is smaller than the known variance
  1. H₀ : s² = ²          H_A : s² > ²  
  2. H₀ : s² = ²          H_A : s² < ²
  3. H₀ : s² = ²          H_A : s² is not equal to ² 
• the third situation is the two tailed test (the alternative hypothesis is simply that the two variances are not equal)

Once again (see the confidence interval above), the² distribution is asymmetric, so the two one-tailed tests use different² values

Procedure:

• First you have to find the² values for each of the three situations (the line numbers correspond to the line numbers above)
• We will use an alpha-level of 0.05 for here as an example, but any alpha-level can be used, of course
• For all three, the degrees of freedom are n - 1   (n = sample size)
  1. if H_A : s² > look up the²  value for 95% (this is a left-tailed test)
  2. if H_A : s² > look up the²  value for 5% (this is a right-tailed test)
  3. if H_A : s² > look up the²  values for 97.5% and 2.5% (this is a two-tailed test)
• calculate the ² statistic

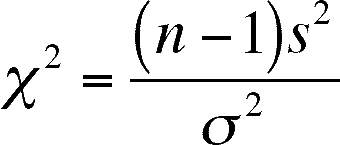
• evaluate the statistic
  1. if H_A : s² > ², accept H₀ if  calculated² > value from the² table, reject H₀ if it is smaller
  2. if H_A : s² < ², accept H₀ if  calculated² < value from the² table, reject H₀ if it is larger
  3. if H_A : s² is not equal to ², accept H₀ if  calculated² > value is between the² table values, reject H₀ if it is outside of the table limits

Situation B - Using the F distribution

We have seen the F distribution before in the lectures on ANOVA

Consider the previous use of the F distribution. 

To evaluate the effect of a factor on a response variable we used the ratio of mean squares, dividing the mean square due to the factor by the mean square due to random error

The ratio is the F statistic, which has a defined probability distribution, and we can compare our F value with a critical value that depends on a pre-defined alpha-level.

A mean square is a variance (look at the way in which it is calculated in Lecture 11a) and so we are really comparing two variances when we calclate the F statistics in an ANOVA table

In other words, we have already compared two variances when we evaluated ANOVA results.  The MS/MS is from lecture 11a and the S/S is the general definition of the F statistic

So, to test for equal variances:

• put the lager of the two variances on top (a ratio below 1 can never be found to be significant)
• find the critical value
• alpha depends on your choice
• degrees of freedom for the numerator is the sample size minus 1
• degrees of freedom for the denominator is also n - 1

Two tailed or one tailed?

You will have to decide if the test is one or two tailed

• one tailed for alternative hypothesis that numerator variance is larger than denominator variance
  • H₀ : s²₁ = s²₂           H_A : s²₁ > s²₂  - note that the one-way always has the numerator greater than the denominator
• two tailed test if the alternative hypothesis is simply that the two variances are not equal
  • H₀ : s²₁ = s²₂           H_A : s²₁ is not equal to s²₂ 
  • for this one, divide alpha level by 2 before looking into the tables for a critical value

To evaluate the F-statistic, you

• accept H₀ if the calculated F-statistic is less than the critical value from the F table
• reject H₀ if the calculated F-statistic is greater than the critical value from the F table

Calculating power

Remember what statistical power is -

The probability of rejecting H₀ when H₀ is false (i. e., when H_A is true).

To test this, we need to know the distribution of t_s when is H_A true

• This is not the same as the distribution of t_s when is H₀ true, which is the t distribution with a mean of 0 and a standard deviation that depends on the degrees of freedom
• When the sample sizes are large (greater than 50 or so), we can use the normal as an approximation of the distribution of t_s (and the probability of rejecting H₀ when H_A is true), just as we could use the same approximation when testing the null hypothesis

Specifics of the test

• Assume that we choose samples (both of size n) from two normally distributed populations with means of ₁ and ₂
• Assume both populations have the same standard deviation,
• If n is large, then the distribution of t_s is approximated as a normal distribution with a

and

standard deviation = 1

• Remember that the normal usually has standard deviation of 1 (same here) but a mean of 0, so this normal curve has been shifted so that it no longer is symmetric about 0 but about a standardized difference between the means
  • When assuming that the null hypothesis is true and testing for that, we expect that there is no difference between the means and so the distribution has 0 as its mean
  • In calculating power, we are assuming that the alternative is true, and we expect that there is a difference between the means (the true difference) and we want the probability distribution to be symmetric about the true difference, which we have estimated above
• Notice that the mean (estimated true difference between the sample means) is related to the ratio of the difference between the means and the true standard deviation -  this was defined in Lecture 7 as the Effect Size
  • the effect size is calculated as is was in Lecture 7, requiring an estimate of both the difference between the means (not the difference between the sample means, but between the true means) and the true standard deviation
  • the true standard deviation and difference between the means are usually estimated from previous experience or calculated through a mathematical model of the situation
  • Notice that the mean will increase as the sample size increases - this is the basis of the method for estimating sample sizes found under the discussion of power in the textbook and in Lecture 7
• So, using t_s (there is only one t_s calculated from any comparison, whether considering power or null hypothesis testing), we can determine the power as the tail of the "shifted" normal distribution.
  • Suppose that we calculate a ts of 2.01 with a n = 49 and an effect size of 0.6
    • the mean  =  sqrt(49/2)*0.6  =  2.97
  • given these figures, we can ask the results from testing the null hypothesis
    • look up 2.01 in the normal table and you see that the upper tail is 0.0222 (1 - 0.9778), so there is only a 2% chance of getting such a large difference between the means if the null hypothesis is true
  • next, look up the power, but shift the normal so that it centers over 2.97, not 0, but the shape is the same and the standard deviation is still 1
    • now 2.01 is to the left of the peak of the normal, whereas it was to the right of it when the curve was centered over 0
    • 2.01 is -0.96 from the  new center of the normal (2.01 - 2.97)
      • remember that the shape of the normal has not changed, so the areas under the curve have not changed either
    • using the normal table, look up -0.96 and you will see that 0.1685 of the curve is to the left of -0.96, so 0.8315 (1 - 0.1685) lies to the right
      • The area to the right is the power, the probability of getting a larger t_s if H_A is true and there is a difference between the means

More post-hoc tests for differences between levels in ANOVA analysis

Sheffé Test

• The Sheffé test compares the means in pairwise fashion
  • all combinations of pairs of means must be tested, which can rapidly build up as the number of means increases
• the procedure is to calculate a F_s value for each pair of means and compare that value to a critical value
  • the critical value for the comparison is an adjusted F value, such that

• where I -1 is the degrees of freedom of the numerator and n - I is the degrees of freedom of the denominator (see Lecture 11a for the definitions of variables)
• once the critical value is known, each F_s is calculated as:

• (where s²_pooled is the MS_within - see Lecture 11a) and the resulting value is compared to the critical value such that
• if F_s > F_critical then reject the null hypothesis of no difference between the means
• if F_s < or = F_critical then accept the null hypothesis of no difference between the means

The Sheffé test is conservative, in that it will reject the null hypothesis less often than other tests provided here and in Lecture 11b

• In fact, the test will sometimes show no differences between any pair of means, even though the ANOVA table indicates that the factor is significant
  • This is due to the fact that the difference detected in the ANOVA may be due to differences between the average of two or more group means compared to other means
• we will not go further than to say that if this situation occurs, it is reasonable to go to another, less conservative, post-hoc test for the difference between group means

Duncan

Dunnett

SNK

Tukey

http://fsweb.berry.edu/academic/education/vbissonnette/tables/posthoc.pdf

http://departments.vassar.edu/~lowry/tabs.html#q

http://cse.niaes.affrc.go.jp/miwa/probcalc/s-range/index.html

Testing for a difference between proportions

Other uses for the Chi-square distribution

We have already gone over two uses above:

• Using the Chi-square distribution to construct a conficence interval for a variance
• Using the Chi-square distribution to test for the difference between a sample and a known variance

A Bit More Probability

We have already had a very brief introduction to probability in Lecture 3 but we will formalize some basic concepts here and introduce some new ones.

Four basic rules of probability:

1.  The probability of an event, x, is expressed as a fraction between 0 and 1, inclusive

0 ≤ Pr(x) ≥ 1

2.  Impossible events have a probability of 0 and certain events have a probability of 1

3.  The sum of the probabilities of all possible events is 1

4.  The compliment of an event (or set of events) is all other possible events (not part of the set) and the probability of the compliment of an event is 1 minus the probability of the event

Pr(compliment x) = 1 - Pr(x)

Adding Probabilities - We have (in Lecture 3) covered the way to add two mutually-exclusive events [Pr(A+B) = Pr(A) + Pr(B)] and how to add two events that are not mutually exclusive [Pr(A+B) = Pr(A) + Pr(B) - Pr(AB)].

• Pr(AB) is the probability that both events will occur (often said "the probability of A and B")
• A moments reflection will show you that these two formulations are really one.  If two events are mutually exclusive, then it stands to reason that Pr(AB) is 0, and the longer equation reduces to the smaller one.

Multiplying Probabilities - In Lecture 3, we introduced multiplying probabilities through the use of a probability tree.  To use the tree, we had to assume that the two events were independent events.

• Pr(A and B) = Pr(A) x Pr(B)

What if the outcome of one event affects the probability of a second event occurring?  We call these dependent events, not surprisingly, and we need a second formula for multiplying these events.

• Want an example of a dependent event?  Take a deck of cards and shuffle it.  Draw out a card. 
• What is the probability that it is an Ace?  If the aces are distributed randomly in the pack, it is 4/52 or 1/13.
• Now, draw a second card without replacing the first. What's the probability it's an Ace.  That depends on the first draw!  If the first draw was not an ace, it's 4/51.  If the first draw was not, it's 3/51 or 1/17. 
• The probability of the second event depends on the outcome of the first.

Dependence in the real world is often more subtle than this example.

• What is the chance that a college student in Nashville goes to TSU?  What is the chance that a student in Nashville will root for the TSU basketball team?  If the first outcome is a yes, the second is close to 1.0, but if the first is a no, the chance is much lower. 
• If this is so, we can say that which basketball team a college student in Nashville roots for depends on the school in which they are enrolled.

So, why and how would we multiply dependent probabilities.  Let's consider a situation in which dependence applies.

Suppose you have a bag of M&M candy, say 10 pieces in the bag.  You are thinking of offering two friends a chance to reach in and choose a piece but are a bit worried.  You like the new blue colored pieces the best and will only offer the candy if the chance of losing two of the blue is sufficiently small.  If there are only 2 blues, how do we calculate the chance that both friends will take a blue (assume that neither can see the piece they are choosing) and leave you bereft of the choicest M&Ms?

The first draw yields a chance of 2/10, or 1/5

Given that the first draw took one of the precious blues, the chance that the second will also be a blue is 1/9. 

We had to reduce both the total number of blue pieces and the total number of pieces by 1 due to the outcome of the first draw.

The probability of both events occurring is then 1/5 x 1/9 or 1/45.  That's low enough for all but the most abject chocoholics and you would probably decide to share.

Suppose you were at a Christmas party where all 10 attendees brought a gift, each with a label indicating who brought it.  Who gets which gift will be decided by writing the attendee's names on identical slips of paper, putting them into a hat, and letting everyone take a slip and open the present they have chosen, even if it's the gift they brought.  During the party, you find out that there are two presents you would really like to have.  When the gift giving begins, you happen to be sitting so that you will be the third person to choose a present.  Before the first person chooses, it occurs to you that both of the desirable presents may be chosen by the time you choose and you ask yourself, "What's the probability of that!"

The chance of a desirable gift being drawn by the first to choose is 2/10 or 1/5.

Given that the first draw took one of the precious gifts, the chance that the second person to choose will take the other good gift is 1/9. 

The probability of both events occurring is then 1/5 times 1/9 or 1/45.  Once you realize this, you stop worrying.

We can formalize this by introducing a new wrinkle in our probability notation, Pr(B|A).  The line is verticle, so it does not indicate a fraction and the expression is read "the probability of event B given that event A has occurred" or, more briefly, "the probability of B given A."

Pr(B|A) is called the conditional probability of B given A.

So, the multiplication of two dependent events is:

Pr (A and B) = Pr(AB) = Pr(A) x Pr(B|A)

To see if you understand, try calculating the following.  Two cards are drawn from a deck and are not replaced.  What is the probabilty of drawing two aces?  of drawing an ace and a king, in that order?  The answers are 4/52 x 3/51 or 12/2652 and 4/52 x 4/52 or 16/2652.

This logic can be extened to three dependent events.  What is the probability of drawing three aces in three cards?  An ace, then a king, then a queen?  The answers here are 4/52 x 3/51 x 2/50 or 24/132,600 and 4/52 x 4/51 x 4/50 or 24/132,600.

The formulation above can be rearranged using some simple algebra.

Reading this in English produces "The probability of B given A is equal to the probability of both A and B occurring divided by the probability of A"

We need to do two things now.  One is to understand what was just said above by going through an example and the next is to understand the implications of this formulation.  The are profound, a term I do not use lightly.

First and example.  This will illustrate the formula and give you some additional experience in the use of a probability tree.  The probability of being born a male Drosophila is 1/2 (their sex determination system is similar to ours).  Suppose that the probability of a Drosophila having the ability to detoxify the insecticide DDT depends on its sex: 1/4 if it's a female but 1/2 if it's a male.

What's the chance that a newly depositied Drosophila egg will be resistant to DDT?

This answer requires the application of the first formulation : Pr (A and B) = Pr(AB) = Pr(A) x Pr(B|A) for each thread of outcomes that leads to a resistant fly.  The diagram

Terminology

Monte Carlo Simulation

This is the basic simulation technique used to simulate long-term real world outcomes based on immediate probabilities of outcomes.

It uses are seen most readily in the description of the Monte Carlo procedure

• determine all possible outcomes from a situation (it could be an experiment or any actual situation)
• determine the probability of each outcome (these probabilities must sum to 1)
• make a scheme that relates a range of random numbers with the probabilities of all outcomes
• if there are three outcomes with the probability of Pr(A) = 0.5, Pr(B) = 0.3, and Pr(C) = 0.2 and the random number range is 0 to 9 (integers), then any of the schemes below will work as well as any other
  1. A = 0, 1, 2, 3, 4     B = 5, 6, 7     C = 8, 9
  2. A = 2, 3, 4, 5, 6     B = 7, 8, 9     C = 0, 1
  3. A = 0, 2, 4, 7, 9     B = 3, 5, 8     C = 1, 6
  • The important feature is that the proportion of the range of random numbers assigned to any outcome is the same as the probability that that outcome will occur
• Select random numbers (from a table or with a good random number generator on a computer - MSExcel has this function but it is not recommended for this use)
• Tally the outcome for each random number choice
• Summarize the outcomes from all choices of random numbers

Markov Chain Simulations

This is a useful method of predicting change in a system over time where there are different states for any member of the system and known probabilities of transitioning from one state to any other state during a given period of time

• for instance, a population of animals can be healthy, sick with a disease, recovered from the disease and immune to further infection, or dead from the disease
• there are four states and you can specify probabilities for transitions between any two states
• some will be zero probabilities (no going from health to recovered or from dead to any other state)

a simulation will begin with a set of individuals, each in one of the four possible states

an iteration will take the situation as it is and move individuals from state to state based on the probabilities of transitioning from the current state to the other states (including no change of state)

successive iterations will simulate the most probable outcome for that system at some time in the future

Markov Chain Monte Carlo Simulations (MCMC Simulations)

If individuals are moved from state to state using a Monte Carlo approach, we refer to the model as an MCMC model