 |
BIOL 3110
Biostatistics Phil Ganter 301 Harned Hall 963-5782 |
| Endemic flower from the Serro do Cipo Mts. in Brazil |
|
 |
BIOL 3110
Biostatistics Phil Ganter 301 Harned Hall 963-5782 |
| Endemic flower from the Serro do Cipo Mts. in Brazil |
|
Comparison of Paired Samples
Chapter 9
| Academic Page | Tennessee State Home page |
| Bio 311 Page | Ganter home page |
Unit Organization:
Problems:
What is meant by Paired?
Whenever two observations are, for some reason, linked such that you suspect that they should be more similar to one another than to the rest of the data, then you have paired observations. A Paired Sample is a set of paired observations.
Paired observations might be before and after samples from the same individual or right side-left side observations from the same individual.
It is not the before-after that makes them paired, but the fact that they came from the same individual.
Paired observations might be from different individuals that have been matched for some set of characteristics (similar size, age, etc.).
What is the Paired Sample t-Test?
The paired test statistic is the difference between the paired observations, which is symbolized by d (for difference).
is average difference. Note that
has the same value as the difference between the means of the two samples (ave. after minus ave. before, etc.).
The mean of the differences is the same as the difference
between the means ( ![]() =
= ![]() 1 -
1 - ![]() 2 ).
2 ).
One can also calculate the standard deviation of d, sd. in the normal way using d as the observations.
The sample size (n) is simply the number of paired observations.
The test asks the question: Is there a difference between the size of the paired observations?
H0 : ![]() = 0
= 0
Ha : ![]() ∫ 0 (non directional)
∫ 0 (non directional)
Standard Error = SEdiff = sdiff /sqrt(n)
The t-value you calculate is like you have done before. It is the ratio of a statistic divided by the standard error.
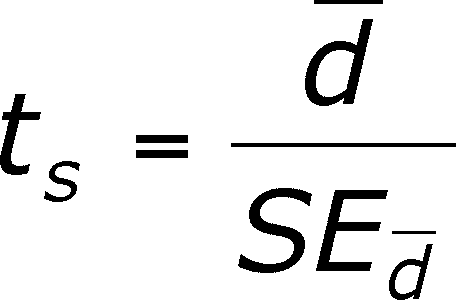
There are n - 1 degrees of freedom.
p-hat = Pr{ts} = The probability of being wrong (committing a type I error) if one rejects H0. As before, one looks up p-hat in the t-table using the value of ts and n-1 degrees of freedom.
Evaluation of Pr{ts} is like any other t-test. If p-hat is smaller than the pre-selected
-value, then the risk of making a mistake is less than the acceptable risk, so you go ahead and reject the null hypothesis. If it is larger, then the risk is greater than you said you would accept.
CONFIDENCE INTERVAL for a paired design
The confidence interval is close to that for a difference between means. The difference lies only in the smaller SE expected for the paired design.
![]() ± ta,df(SEd)
± ta,df(SEd)
The t value depends on the chosen alpha value and the degrees of freedom, which are the same as above (n-1)
Under what assumptions is it fair to use a paired design?
First, you must suspect that the pairing are reasonable. Then the assumptions are the same as for the t-test in general.
d must be calculated from a random sample.
the d's must be distributed normally when the sample size is small. This assumption is relaxed as the sample size gets large due to the effect of the central limit theorem.
Why do we do a paired t-test rather than a regular comparison of sample means?
There are two reasons for using a paired design: reduction of bias and/or increased precision. Both reasons may be true at once.
The difference in the outcome usually lies in the standard error of d being smaller than the standard error of the difference between the means (although the degrees of freedom is usually greater in the second case).
This area can be best explained with two examples.
Reduction of bias.
Suppose that you are conducting an experiment in which plant size is being compared for plants treated with a pesticide versus control plants without treatment. You are going to grow the plants in pots on a table in a room with a large window on one side. The 24 pots will fill the table in six rows of four pots, with the side of the table with 4 pots parallel to the window. You suspect that the plants in pots on the side of the table away from the window will get less sunlight in general and will be smaller. Thus, you suspect that bias is part of the design because there is a systematic difference in growth due to pot position.
A randomized blocks design is a way of reducing bias. But how to block? I suggest that you use small blocks: Pairs of pots. Each pair is a pot in an even row with a pot next to it in the next row away from the window. Thus, the first two rows make up four blocks as in the diagram:
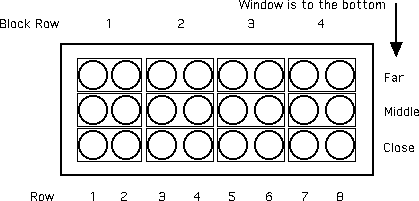
Each pair of circles in a small rectangle represents a block. Treatment or control is assigned randomly to each pot. The idea here is that there will be little difference between row 1 and 2 (compared to the difference between 1 and 8) and you will be allocating randomly within the block. Now you have 12 pairs of observations (linked by being in the same block) and can used a paired design. Look at the results (cooked up by me) and you will see that there was bias in the design (notice that the far plants are much smaller, as predicted).
| Position | Block | Treated | Control | d |
| Close | 1 | 57 | 52 | 5 |
| Close | 2 | 56 | 55 | 1 |
| Close | 3 | 57 | 53 | 4 |
| Close | 4 | 59 | 56 | 3 |
| Middle | 5 | 37 | 32 | 5 |
| Middle | 6 | 36 | 35 | 1 |
| Middle | 7 | 37 | 33 | 4 |
| Middle | 8 | 39 | 36 | 3 |
| Far | 9 | 17 | 12 | 5 |
| Far | 10 | 16 | 15 | 1 |
| Far | 11 | 18 | 13 | 5 |
| Far | 12 | 19 | 16 | 3 |
| mean | 37.33 | 34.00 | 3.33 | |
| St Dev | 16.99 | 17.14 | 1.61 | |
| n | 12 | 12 | 12 | |
| SE | 4.90 | 4.95 | 0.47 | |
| difference in means | 3.33 | |||
| unpooled SE | 2.01 | |||
| ts for paired comparison | 7.15 | |||
| ts for unpaired comparison | 1.66 | |||
| d.f. for paired comparison | 11 | |||
| d.f. for unpaired comparison | 22 | |||
| p-value for paired | 0.00002 | |||
| p-value for unpaired | 0.11 | |||
Notice that I have calculated p-hat for two different scenarios: a paired design and an unpaired design.
The standard error of
(0.47) is much smaller than the unpooled SE for the difference between means (2.01) so the ts-value for
is much larger because the SE's are different while the numerators are not.
Thus, p-hat is much less for the paired design than for the unpaired design (remember that this is an extreme case with cooked data).
Increase in Precision
Here, we will just give some numbers for an undescribed experiment with two samples, each with six replicate samples. Assume that the six can be paired and look at the difference in the analysis depending on whether or not the observations are paired.
| Treated | Control | d | |
| 36 | 29 | 7 | |
| 57 | 43 | 14 | |
| 99 | 83 | 16 | |
| 23 | 11 | 12 | |
| 45 | 32 | 13 | |
| 71 | 64 | 7 | |
| mean | 55.17 | 43.67 | 11.50 |
| St Dev | 27.13 | 26.00 | 3.73 |
| n | 6 | 6 | 6 |
| SE | 11.08 | 10.61 | 1.52 |
| difference in means | 11.50 | ||
| unpooled SE | 6.26 | ||
| ts for paired comparison | 7.56 | ||
| ts for unpaired comparison | 1.84 | ||
| d.f. for paired comparison | 5 | ||
| d.f. for unpaired comparison | 10 | ||
| p-value for paired | < 0.001 | ||
| p-value for unpaired | > 0.10 | ||
In this case, just look at the two samples and notice that in both there is a lot of variation between observations within each sample. This makes the unpooled standard error large. However, the differences (d's) show much less variation and so their standard error is much smaller. This leads to very different p-hat values.
A Nonparametric Approach: the Sign Test
This test is useful when sample size is small and there are real doubts about whether or not a t-test can be used.
It is based on the sign of the difference between paired observations.
Let's restate the null and alternative hypotheses so that we are clear:
H0 : ![]() = 0
= 0
HA : ![]() € 0
€ 0
If H0 is true, then the error between the observations is random. If this is so, then there should be an equal chance of getting a positive difference or a negative difference. That is, we expect half of the signs to be + and half to be -.
The signs test is based on this assumption and the binomial distribution.
If we have n pairs, then half of the pairs should yield + d's and half should yield - d's.
The probability (
) of getting a + or a - in each case is 0.5.
If we actually get j positives, what is the probability of that?
This is a binomial, with
= 0.5 and we are asking about j successes in n trials
Remember that we are dealing with the probability in the tail of the distribution, so we need to include not just the probability of getting j successes but also the probability of getting all of the successes in the tail. This means you should draw the tails out and figure out which probabilities you need to calculate.
What to do with tied pairs, so that d = 0.
Ignore them. Remove them from the dataset and proceed as above.
Evaluation
In order to make this into a test that is equivalent to the t-test, we have to have a criterion for accepting or rejecting the null.
We will use the same one but it is not exactly straight forward. First, select an
-value.
Nondirectional
Suppose that there are 20 d's and we get 17 -'s and 3+'s.
If the sum of the probability of getting 17 or more minuses (notice that this includes J = 17, 18, 19, and 20) plus the probability of getting 3 or fewer minuses (j = 3, 2, 1 or 0) is less than
, then we will reject H0.
Why 17 or more minuses? Because the tail of the distrubution includes all of these values of j!
Why 3 or fewer minuses? Because, for a nondirectional test, we need both tails, and 3 to 0 is the lower tail that corresponds to 17 to 20, the upper tail!
Directional
Using the example above, we first must decide which direction is of interest. Lets look at the possible HA's
HA :
> 0
Since there are 17 -'s, then the average d must be a negative number, which means our alternative can't be true, so nothing more need be done.
HA :
< 0
If the sum of the probability of getting 17 or more -'s is less than
then we reject H0.
You can also use table 7 in the book, but it is not as exact as the procedure above.
When can you use the signs test?
There are few assumptions.
If it is reasonable to assume that the d's are as likely to be positive as negative, then the test is valid.
No particular distribution is assumed.
However, you should realize that much information is in the data that is not being used for this test, which makes it's power lower than that of a parametric test like the t- test.
The lack of power (as defined in an earlier lecture) means that you are more likely to accept H0 when it is false.
A Nonparametric Approach: the Wilcoxson Signed-Rank Test
This uses a bit more information than does the signs test, so it is a bit more powerful.
To do this test, rank the d's from smallest to largest (based on their absolute value).
Restore the + and - signs.
Add the negative ranks and take their absolute value.
Add the positive ranks.
The test statistic (Ws)is whichever is the larger of the two sums above.
Evaluation
The null and alternative hypotheses are as for the signs or t-test.
We will use the same one but it is not exactly straight forward. First, select an
-value.
Nondirectional
Reject the null if Ws is larger than the Table 8 entry for n and the two-way
.
Directional
First must decide which direction is of interest. Lets look at the possible HA's
HA :
> 0
If Ws is the summed positive ranks, then it makes sense to proceed with the test. If Ws is the summed negative ranks, then d was usually negative and it makes no sense to perform the test.
Reject the null if Ws is larger than the Table 8 entry for n and the one-way
.
HA :
< 0
If Ws is the summed negative ranks, then it makes sense to proceed with the test. If Ws is the summed positive ranks, then d was usually positive and it makes no sense to perform the test.
Reject the null if Ws is larger than the Table 8 entry for n and the one-way
.
When can you use the Wilcoxson Signed-Ranks test?
There are few assumptions.
If it is reasonable to assume that the d's are as likely to be positive as negative, then the test is valid.
No particular distribution is assumed.
Last updated March 30, 2006